Homework #2

Group Members:

Mei Fun Wong

Meng Yi Yee

Carrie Neer

 

  1. (10 points) Consider the following EBNF syntax. Which if the sentences following are not legal according to the syntax for sneeches? Why?
sneech ::= '*' |( '(' <sneech> ')' '*') |[ <bander>] <sneech>
bander ::= { '+$+' | '#' } | ('%' <bander> )
1. (*) Not Legal would have to either be (*)* using sneech ::=(’(‘<sneech>’)’’*’) or * using sneech ::=’*’ to be legal
2. (+$+*) Not Legal there are extra parenthesis if sneech::=[<bander>]<sneech> or it is missing an asterisk (ie. (+$+**) if sneech""= (’(‘<sneech>’)’’*’) were used
3. * Legal it is legal when sneech::=’*’ is used
4. ***** Not Legal cannot have repeating sneec
5. %%%** Not Legal ‘*’ would not be generated using bander::=(‘%’<bander>)
6. #####** Not Legal it is not possible to have repeating sneech (ie. ** ), it is only possible to have #####* or #####(*)* using sneech::=[<bander>]<sneech>
7. (+$+# Not Legal there is no way it could be generated since there is only one parenthesis
8. +$+#* Legal is legal if sneech::[<bander>]<sneech> is used
9. *+$+# Not Legal there is not way it could be generated since it starts with a sneech, * and no parenthesis
10. %#*+$+** Not Legal starting with sneech::=[<bander>]<sneech> you get to the first aster isk hit a dead-end using sneech::=’*’

 

2. (5 points) Consider the grammer

bexpr ::= bexpr or bterm | bterm
bterm ::= bterm and bfactor | bfactor
bfactor ::= not bfactor | (bexpr) | true | false

Construct a parse tree for the sentence not (true or false).
Show that this grammar generates all boolean expressions.

bexpr => bterm => bfactor => not bfactor => not (bexpr) => not (bexpr or bterm)

=> not (bterm or bterm) => not (bfactor or bfactor) => not (true or false)

 

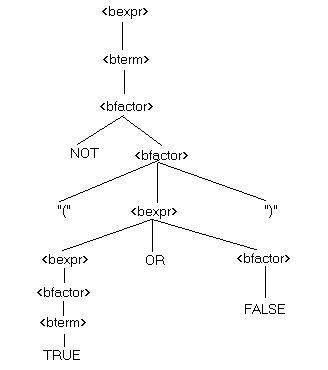
By traversing the tree, the tree generated will lead to bfactor which will generates all boolean expression.

bexpr=> bterm=> bfactor=> true

bexpr=> bterm=> bfactor=>false

bexpr=> bterm=> bfactor=> not bfactor=> not true

bexpr=> bterm=> bfactor=> not bfactor=> not false

bexpr=> bexpr or bterm=> bterm or bterm=> bfactor or bfactor=> true or false

bexpr=> bexpr and bterm=> bterm and bterm=> bfactor and bfactor=> true and false

bexpr => bterm => bfactor => not bfactor => not (bexpr) => not (bexpr or bterm)

=> not (bterm or bterm) => not (bfactor or bfactor) => not (true or false)

 

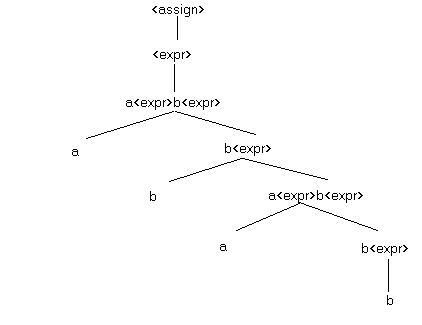
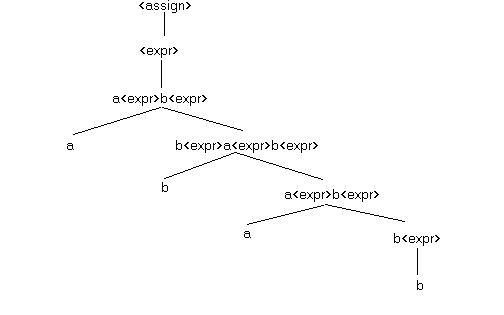
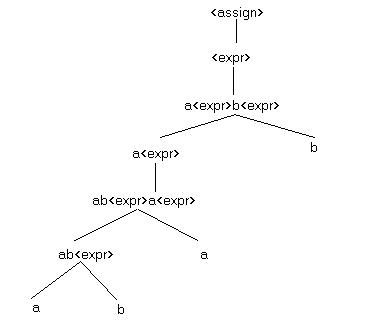
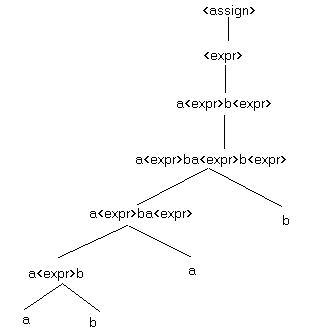
3. (10 points) Consider the grammar:

S ::= aSbS | bSaS | empty

Show that this grammar is ambiguous by constructing two different leftmost derivations for the sentence abab.
Construct the corresponding rightmost derivations for abab.
Construct the corresponding parse trees for abab.

Leftmost Derivations

<assign> => <expr>
=> a<expr>b<expr> => ab<expr>
=> aba<expr>b<expr>
=> abab<expr>
=> abab

 

 
<assign> => <expr>
=> a<expr>b<expr>
=> ab<expr>a<expr>b<expr >
=> aba<expr>b<expr>
=> abab<expr>
=> abab

 

Rightmost Derivation

<assign> => <expr>
=> a<expr>b<expr>
=> a<expr>b
=> ab<expr>a<expr>b
=> ab<expr>ab
=> abab

 

 
<assign> => <expr>
=> a<expr>b<expr>
=> a<expr>ba<expr>b<expr>
=> a<expr>ba<expr>b
=> a<expr>bab
=> abab

 

 

4. (30 points) Construct a grammar for if-then statements of each of the following languages:

Java, JavaScript, C++

<if_statement> ::= IF "(" <boolean_expression> ")" "{"<statement_seq uence> "}"
{ELSE IF "("<boolean_expression> ")" "{" <statement_sequence> "}" }
[ ELSE "{" <statement_sequence> "}" ]

Prolog

<id statemen>::=<result>:-condition

Lisp

<if_statement> ::= "(" IF <test_exp> "("<then_stmt>")" [ <else_stmt> ] ")"
| "(" COND "(" <test_exp><then_stmt>")" "(" "t" <else_stmt> ")" ")"

Eiffel

<if_statement> ::= IF<boolean_expression> THEN <statements>
{ELSEIF <boolean_expression> THEN <statements>}
[ ELSE <statements> ]
END